5.15 Assignments
|
(6) Part I Write a program that computes all factorials 1!, 2!, 3!, ... up to a number input from the keyboard. Declare all variables to be int. Enter the number 17 from the keyboard and, using the fact that an int is a 4-byte quantity in the gnu compiler, explain the output values by the program. Example: > ./program Enter the number of factorials desired: 17 Output: ... 10! = 3628800 11! = 39916800 12! = 479001600 13! = 1932053504 14! = 1278945280 15! = 2004310016 16! = 2004189184 17! = -288522240 Explanation The program begins producing incorrect results at 13! because the int data type is a 4-byte signed integer in the gnu compiler. Any number that is greater than the upper bound of 231-1 will not fit into a variable of int type, and any attempt to do so will result in an overflow and erroneous results. |
Source Code |
|
(6) Part II Now show that, by changing a single variable declaration from int to double, you can reproduce the correct result for the first 17 factorials. Example: > ./program Enter the number of factorials desired: 17 Output: ... 10! = 3.62880e+06 11! = 3.99168e+07 12! = 4.79002e+08 13! = 6.22702e+09 14! = 8.71783e+10 15! = 1.30767e+12 16! = 2.09228e+13 17! = 3.55687e+14 Explanation Changing the declaration of variable "T" from int to double, provides a much greater range. |
Source Code |
|
(7) Part I Type in and run the following program, which calculates the magnitude of the gravitational field of a point particle with a mass equal to the Earth's mass and display the results as either a contour plot, a color graph, or a three-dimensional line plot. Example Plot: 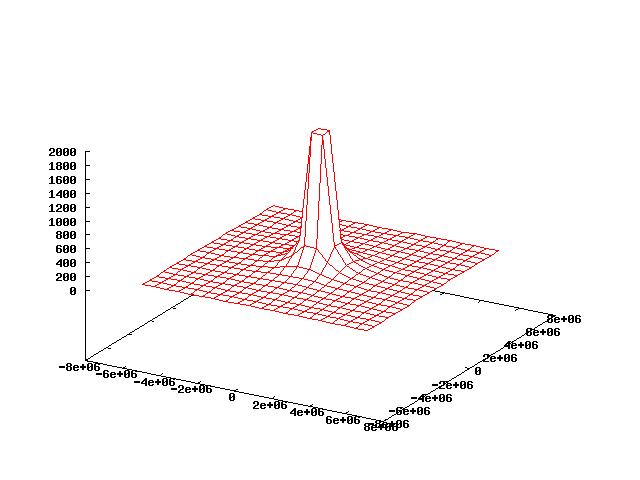
|
Source Code |
|
(7) Part II Modified C++ program to yield the correct magnitude of the gravitational field both inside and outside of a spherical Earth of constant density. Example Plot: 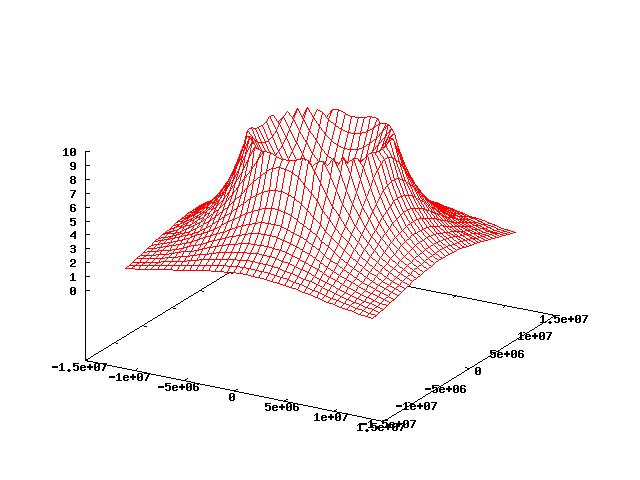
|
Source Code |