Introduction to Numerical Differential Equations
|
In this exercise, the radioactive decay of nuclei was studied. The Euler-Cromer method was used to generate an incremental equation from the differential equations governing radioactive decay, and the fraction of nuclei remaining versus time were calculated numerically through successive iterations for given mean lifetimes of the nuclei involved. 
|
Source Code |
|
Consider a system of a parent, P, and a daughter nucleus,
D, both radioactive: Source Code
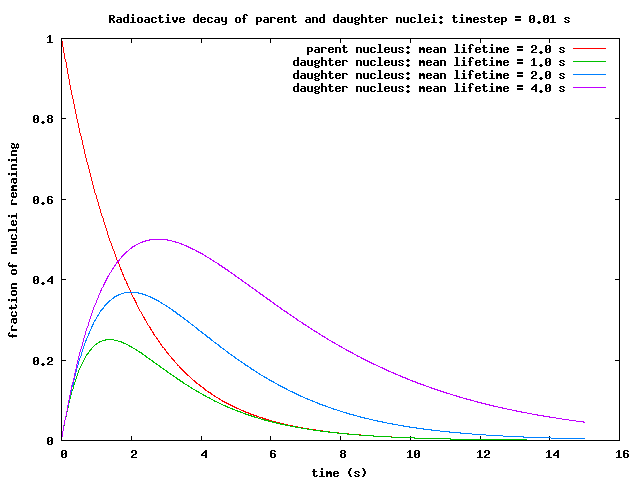
Shawn Havery (PHZ4151C in Spring 2008): It can be seen that, in all three cases, the fraction of daughter nuclei initially increases as parent nuclei decay into daughter nuclei. At some point, however, the fraction of remaining parent nuclei becomes too low to sustain an increase in daughter nuclei, as the daughter nuclei are decaying faster than they are being produced. The point where this occurs depends on the mean lifetime of the daughter nucleus relative to that of the parent nucleus: If the mean lifetime of the daughter nucleus is less than that of its parent, then the peak in daughter nuclei occurs below the quantity of parent nuclei present at that time. Likewise, if the mean lifetime of the daughter nucleus is greater than that of its parent, then the peak in daughter nuclei occurs above the quantity of parent nuclei present at that time. If, however, the mean lifetimes of parent and daughter nuclei are equal, then the quantities of both types of nuclei are equal at the point of peak daughter nuclei. This is because, in this scenario, both types of nuclei have the same mean lifetime, and thus are decaying at the same rate. |
|